System Earth 1b

A planet in and out of equilibrium

Misha Velthuis

m.velthuis@uva.nl

Fri 6 Sept 2024

Recap

Link to recommendations

(Feel free to add/edit!)

Content

Systems thinking

Stocks and flows

Feedback loops

Modeling dynamic equilibria (analytical and numerical)

Perturbations and forcings

Adding features: connected systems + feedback factor

Systems thinking

Tendency to focus on how things connect

Tendency to zoom out

Stocks and flows

Basics

Dynamic equilibria

Average residence time

We are all dynamic equilibria

Stocks influencing flows

Me adjusting how much I eat per day

on the basis of how much I weigh

Numbers of deaths per year going up

as the population increases

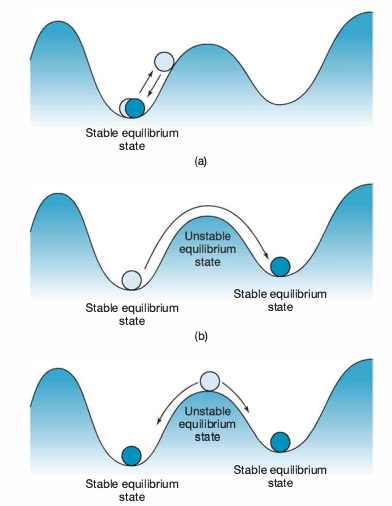
Feedback loops

Positive and negative couplings

Positive feedback loop:

Change A causes change B

which strengthens change A

Negative feedback loop

Change A causes change B,

which dampens change A

Breaking down in couplings

Positive coupling: –>

Negative coupling: –o

Combining couplings

Positive + positive = positive feedback

Positive + negative = negative feedback

Negative + negative = positive feedback

Spiral of love

happiness A –> happiness B

happiness B –> happiness A

Spiral of toxic comparison

happiness A –o happiness B

happiness B –o happiness A

Stability of a weird friendship

happiness A –> happiness B

happiness B –o happiness A

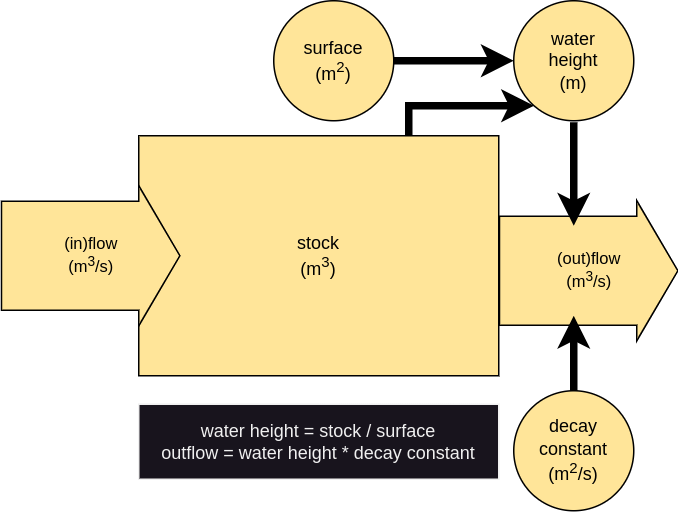
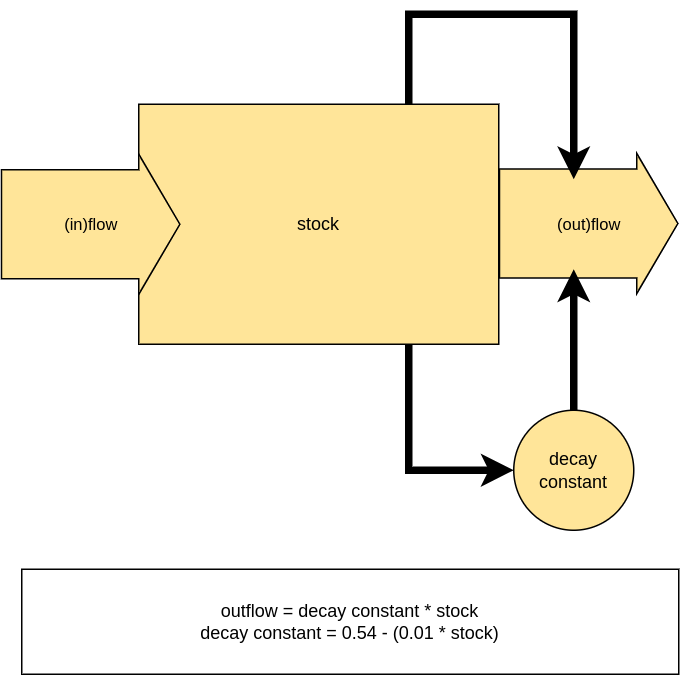
Stability of a reservoir

In short: change A causes change B, which dampens change A.

If the water height is a higher than the equilibrium water height, the pressure at the outlet will be relatively high, which will cause the outflow to be relatively high. As the outflow is higher than the inflow, the water height will go down, towards the equilibrium water height.

If the water height is a lower than the equilibrium water height, the pressure at the outlet will be relatively low, which will cause the outflow to be relatively low. As the outflow is lower than the inflow, the water height will go up, towards the equilibrium water height.

As the water height approaches the equilibrium water height, the difference between the outflow and the inflow will get smaller, which will slow down the speed at which the water height approaches the equilibrium water height.

So again, in short: change A (water height approaching the equilibrium water height) causes change B (reduction of difference between outflow and inflow), which dampens change A (water height approaching the equilibrium water height).

Recap of (part of) calculus

What is Euler's e?

The e of Earth: growth #1

When the growth/decay of something depends on the size of something.

import os
import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 4, 200)
y = np.e**t

# PLOTTING

plt.plot(t, y)

# Draw vertical lines at t=1, t=2 and t=3
for x in [1, 2, 3]:
    plt.axvline(x=x, color='r', linestyle='--')

# Calculate and annotate intersection y-values 
for x in [1, 2, 3]:
    y_val = np.e**x
    plt.plot(x, y_val, 'bo') # blue circle at intersection
    plt.text(x, y_val, f'y={y_val:.2f} ($e^{x}$)', ha='right') # 2 decimal places for readability

plt.title('Growth = Size')
plt.xlabel('Time (t)')
plt.ylabel('Size (S)')
plt.grid(True)
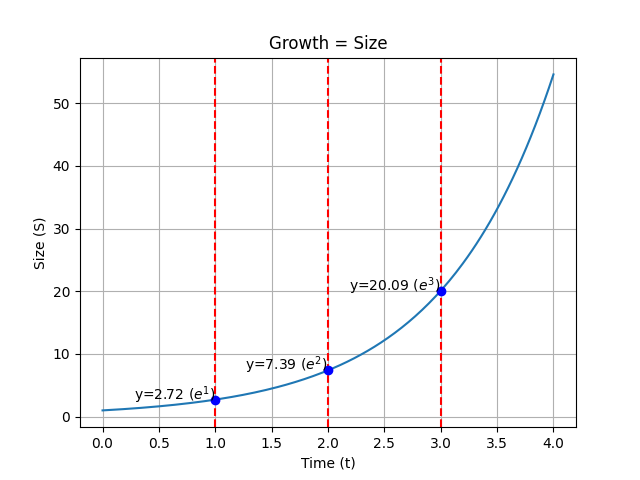
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/exp-growth.png")
plt.close()

When…

\(\delta{}S/\delta{}t = S\)

then …

\(S(t) = e^{t}\)

In other words, when the value of the speed at which something grows is - at every point in time - equal to the value of its size, it will be …

… e times bigger after one time unit
… e² times bigger after two time units
… e³ times bigger after three time units.
Etc…

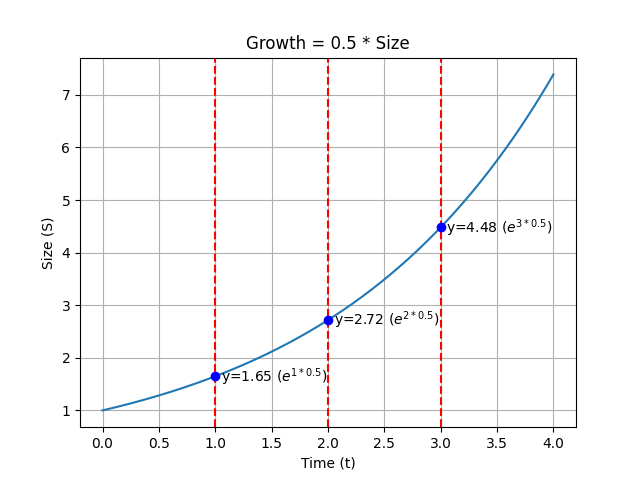
The e of Earth: growth #2

import os
import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 4, 200)
y = np.exp(0.5*t)

# PLOTTING

plt.plot(t, y)

# Draw vertical lines at t=1, t=2 and t=3
for x in [1, 2, 3]:
    plt.axvline(x=x, color='r', linestyle='--')

# Calculate and annotate intersection y-values 
for x in [1, 2, 3]:
    y_val = np.e**(x*0.5)
    plt.plot(x, y_val, 'bo') # blue circle at intersection
    plt.text(x+0.05, y_val-0.1, "y=%s ($e^{%s*0.5}$)" % (round(y_val,2),x), ha='left') # 2 decimal places for readability

plt.title('Growth = 0.5 * Size')
plt.xlabel('Time (t)')
plt.ylabel('Size (S)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/exp-growth2.png")
plt.close()

When…

\(\delta{}S/\delta{}t = 0.5*S\)

then …

\(S(t) = e^{0.5*t}\)

When the value of the speed at which something grows is - at every point in time - equal to half the value of its size, it will be

… e^1*0.5 times bigger after one time unit
… e^2*0.5 times bigger after two time units
… e^3*0.5 times bigger after three time units

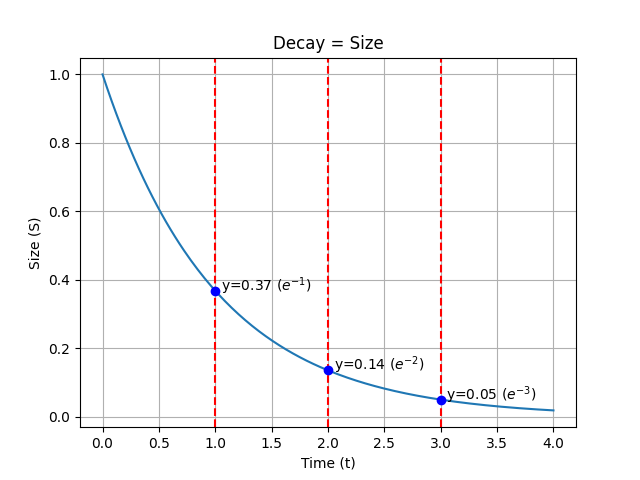
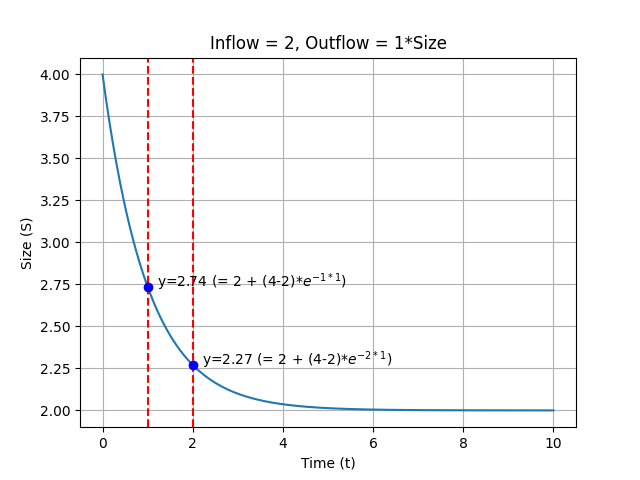
The e of Earth: decay #1

import os
import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 4, 200)
y = np.e**(-t)

# PLOTTING

plt.plot(t, y)

# Draw vertical lines at t=1, t=2 and t=3
for x in [1, 2, 3]:
    plt.axvline(x=x, color='r', linestyle='--')

# Calculate and annotate intersection y-values 
for x in [1, 2, 3]:
    y_val = np.e**(-x)
    plt.plot(x, y_val, 'bo') # blue circle at intersection
    plt.text(x+0.05, y_val, "y=%s ($e^{-%s}$)" % (round(y_val,2),x), ha='left') # 2 decimal places for readability

plt.title('Decay = Size')
plt.xlabel('Time (t)')
plt.ylabel('Size (S)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/exp-decay.png")
plt.close()

When…

\(\delta{}S/\delta{}t = -S\)

then …

\(S(t) = e^{-t}\)

When the value of the speed at which something decays is - at every point in time - equal to the value of its size, it will have …

… diminished by a factor e^-1 (= 1/e) after one time unit
… diminished by a factor e^-2 (= 1/e²) after two time units
… diminished by a factor e^-3 (= 1/e³) after three time units
… etc.

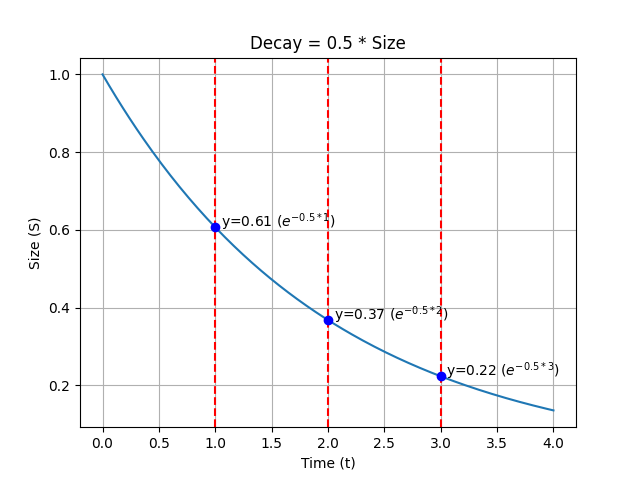
The e of Earth: decay #2

import os
import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 4, 200)
y = np.e**(-0.5*t)

# PLOTTING

plt.plot(t, y)

# Draw vertical lines at t=1, t=2 and t=3
for x in [1, 2, 3]:
    plt.axvline(x=x, color='r', linestyle='--')

# Calculate and annotate intersection y-values 
for x in [1, 2, 3]:
    y_val = np.e**(x*-0.5)
    plt.plot(x, y_val, 'bo') # blue circle at intersection
    plt.text(x+0.05, y_val, "y=%s ($e^{-0.5*%s}$)" % (round(y_val,2),x), ha='left') # 2 decimal places for readability

plt.title('Decay = 0.5 * Size')
plt.xlabel('Time (t)')
plt.ylabel('Size (S)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/exp-decay2.png")
plt.close()

When…

\(\delta{}S/\delta{}t = -0.5*S\)

… i.e. a decay constant of 0.5 …

then …

\(S(t) = e^{-t*0.5}\)

When the value of the speed at which something grows is - at every point in time - equal to half the value of its size, it will be

… diminished by a factor e^1*0.5 after one time unit
… diminished by a factor e^2*0.5 after two time units
… diminished by a factor e^3*0.5 after three time units
… etc.

Reservoir: constant inflow, variable outflow

Let's take a reservoir with an inflow of 2, and an outflow that is equal to \(DC\) (decay constant) times the Size.

\(\delta{}S/\delta{}t = 2-DC*S\)

then …

\(S(t) = S_{eq} + dev_{init} * S_{eq} * e^{-t*DC}\)

Where…

\(S_{eq}\) is the Size at which inflow is equal to outflow (= \(inflow/DC\))

\(dev_{init}\) = the number of times \(S_{eq}\) the reservoir starts above (or below) the \(S_{eq}\).

import os
import numpy as np
import matplotlib.pyplot as plt

inflow = 2
DC = 1

S_eq = inflow/DC
dev_init = 1

t = np.linspace(0, 10, 800)
y = S_eq + dev_init*S_eq*np.e**(-DC*t)

# PLOTTING

plt.plot(t, y)

# Draw vertical lines at t=1 and t=2
for x in [1, 2]:
    plt.axvline(x=x, color='r', linestyle='--')

# Calculate and annotate intersection y-values 
for x in [1, 2]:
    y_val = S_eq + dev_init*S_eq*np.e**(-DC*x)
    plt.plot(x, y_val, 'bo') # blue circle at intersection

    plt.text(x+0.2, y_val, "y=%s (= 2 + (4-2)*$e^{-%s*%s}$)" % (round(y_val,2),x,DC), ha='left')    

plt.title('Inflow = 2, Outflow = %s*Size' % DC)
plt.xlabel('Time (t)')
plt.ylabel('Size (S)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/exp-decay3.png")
plt.close()

In general, any deviation from the equilibrium will be reduced to \(e^{-t*DC}\) of it's original size, after t time units.

In this example (where \(DC\) = 1, and the original deviation from the \(S_eq\) is (4-2=2)):

after one time unit, S = 2+(4-2)*(e^-1*1) = 2.74
- the original deviation from S_eq (2) is reduced to 1/e of its size (2*(1/e)=0.74)
after two time units, S = 2+(4-2)*(e^-1*2) = 2.27
- the original deviation from S_eq (2) is reduced to 1/e² of its size (2*(1/(e²))=0.27)

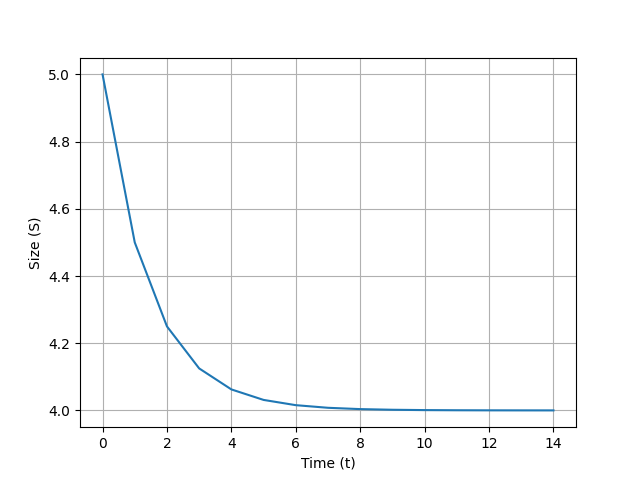
Numerical solutions: the easy way out

Code in Python

# Amount added every timestep
inflow = 2 
# Fraction of S that flows out, every timestep
DC = 0.5

# Model runs until this time
t_end=15
# Length of each timestep
dt=1
# Create list of time
time=np.arange(0,t_end,dt)

# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 6
# For every item in the List time
for t in time:
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to current stock size
    S=S+(dS*dt)
    # Append the new stock size
    S_store.append(S)

Code in Python with graph

import numpy as np
import matplotlib.pyplot as plt

# Amount added every timestep
inflow = 2 
# Fraction of S that flows out, every timestep
DC = 0.5

# Model runs until this time
t_end=15
# Length of each timestep
dt=1
# Create list of time
time=np.arange(0,t_end,dt)

# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 6
# For every item in the List time
for t in time:
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    # Append the new stock size
    S_store.append(S)

# PLOTTING
plt.plot(time,S_store)
plt.xlabel('Time (t)')
plt.ylabel('Size (S)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/numerical-example.png")
plt.close()

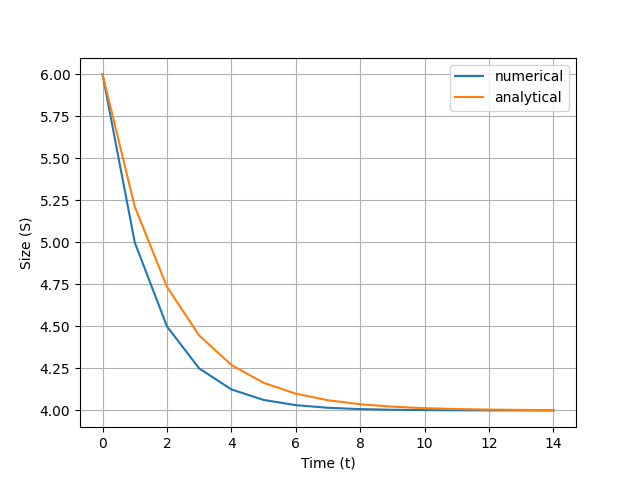
Compare numerical and analytic

import numpy as np
import matplotlib.pyplot as plt

# Amount added every timestep
inflow = 2 
# Fraction of S that flows out, every timestep
DC = 0.5

# Model runs until this time
t_end=15
# Length of each timestep
dt=1
# Create list of time
time=np.arange(0,t_end,dt)

# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 6
# For every item in the List time
for t in time:
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    # Append the new stock size
    S_store.append(S)

# ANALYTICAL SOLUTION
# Determine equilibrium stock size (at which inflow = outflow)
S_eq = inflow/DC 
S_init = 6
# Determine how many times the S_eq above/below the S_eq the S starts
diff_init = (S_init-S_eq)/S_eq
S2=S_eq + diff_init*S_eq*np.e**(-time*DC)
# at t=0, np.E**(0) = 1, so if factor is 1, you get Eq_S - Eq_S which is 0

# PLOTTING
plt.plot(time,S_store,label='numerical')
plt.plot(time,S2,label='analytical')
plt.xlabel('Time (t)')
plt.ylabel('Size (S)')
plt.grid(True)
plt.legend()
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/numerical-analytic-example.png")
plt.close()

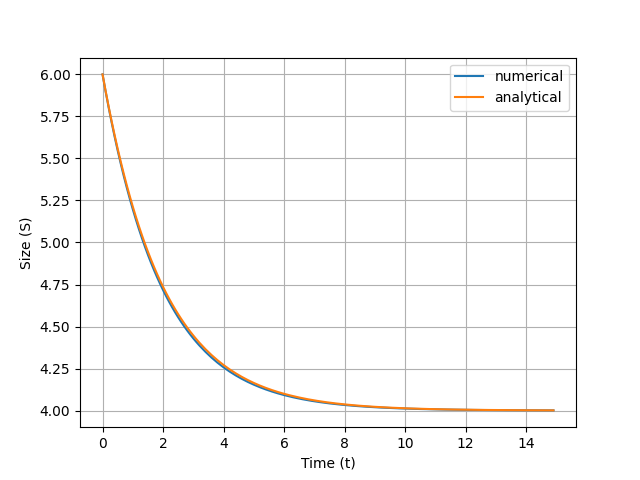
Compare numerical and analytic

import numpy as np
import matplotlib.pyplot as plt

# Amount added every timestep
inflow = 2 
# Fraction of S that flows out, every timestep
DC = 0.5

# Model runs until this time
t_end=15
# Length of each timestep
dt=0.1
# Create list of time
time=np.arange(0,t_end,dt)

# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 6
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)

# ANALYTICAL SOLUTION
# Determine equilibrium stock size (at which inflow = outflow)
S_eq = inflow/DC 
S_init = 6
# Determine how many times the S_eq above/below the S_eq the S starts
diff_init = (S_init-S_eq)/S_eq
S2=S_eq + diff_init*S_eq*np.e**(-time*DC)
# at t=0, np.E**(0) = 1, so if factor is 1, you get Eq_S - Eq_S which is 0

# PLOTTING
plt.plot(time,S_store,label='numerical')
plt.plot(time,S2,label='analytical')
plt.xlabel('Time (t)')
plt.ylabel('Size (S)')
plt.grid(True)
plt.legend()
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/numerical-analytic-example-small-dt.png")
plt.close()

smaller \(\delta{}t\)

Perturbations and forcings

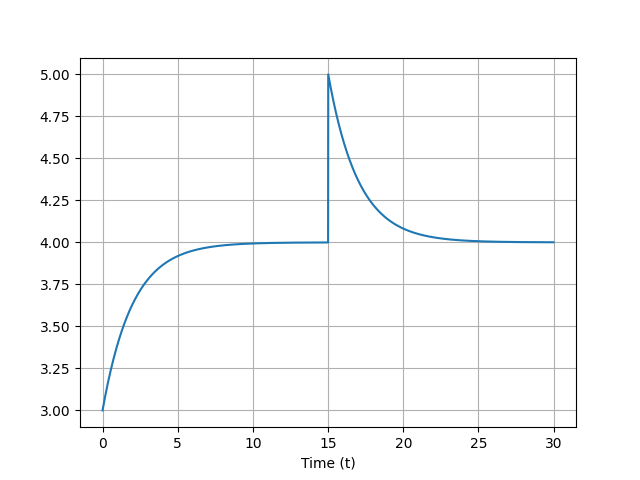Perturbation

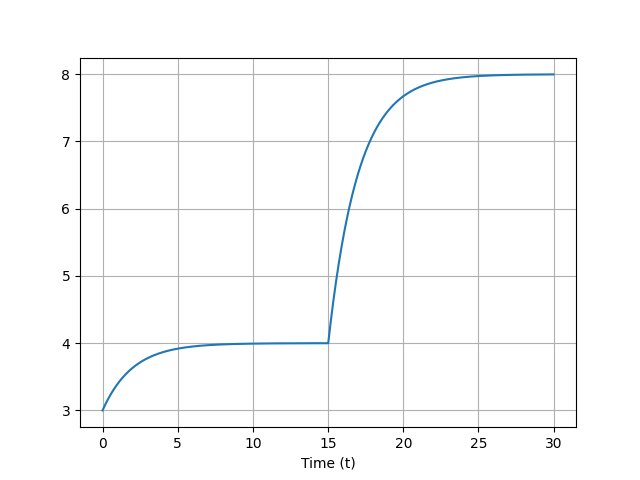Forcing:

Perturbation:


import numpy as np
import matplotlib.pyplot as plt

S_init = 3 # Initial stock size
inflow = 2
DC = 0.5

# Configure time
t_end=30
dt=0.01
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = S_init 
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    if t == 15:
        S=S+1

# PLOTTING
plt.plot(time,S_store)
plt.xlabel('Time (t)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/perturbation.png")
plt.close()

Forcing:


import numpy as np
import matplotlib.pyplot as plt

S_init = 3 # Initial stock size
inflow = 2
DC = 0.5

# Configure time
t_end=30
dt=0.01
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = S_init 
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    if t == 15:
        inflow = inflow + 2

# PLOTTING
plt.plot(time,S_store)
plt.xlabel('Time (t)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/forcing.png")
plt.close()

Admittedly: what appears to be a forcing on a short timescale can appear like a perturbation on a long timescale.

Response time

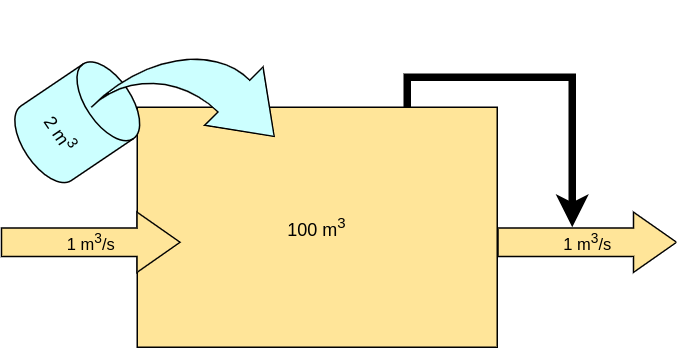
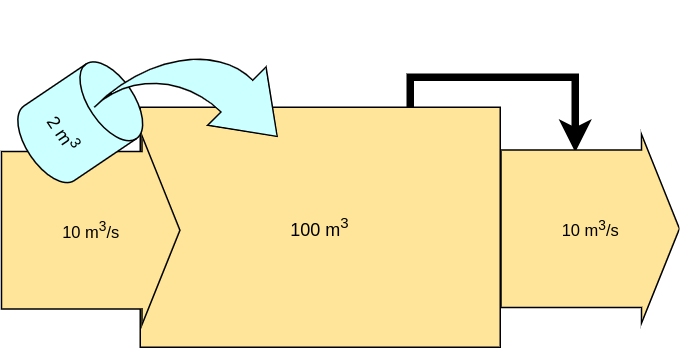
Let's see …

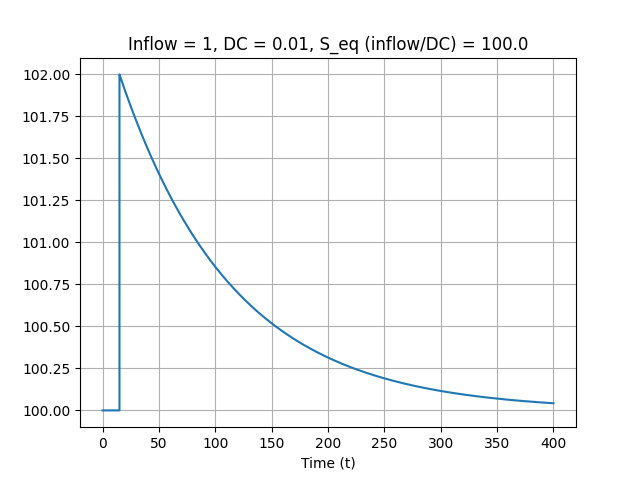Small inflow, relative to equilibrium stock size

Large average residence time

Large response time

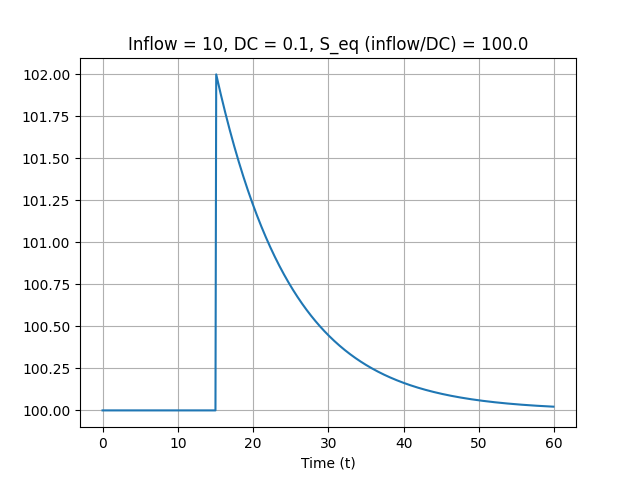Large inflow, relative to equilibrium stock size

Small average residence time

Small response time

Perturbation with relative small flows compared to equilibrium stock size (large average residence time).


import numpy as np
import matplotlib.pyplot as plt

inflow = 1
DC = 0.01

# Configure time
t_end=400
dt=0.01
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 100
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    if t == 15:
        S=S+2

# PLOTTING
plt.title("Inflow = %s, DC = %s, S_eq (inflow/DC) = %s" % (inflow, DC,inflow/DC))
plt.plot(time,S_store)
plt.xlabel('Time (t)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/perturbation-small-flow.png")
plt.close()

Perturbation with relative large flows compared to equilibrium stock size (small average residence time).


import numpy as np
import matplotlib.pyplot as plt

inflow = 10
DC = 0.1

# Configure time
t_end=60
dt=0.1
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 100
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    if t == 15:
        S=S+2

# PLOTTING
plt.title("Inflow = %s, DC = %s, S_eq (inflow/DC) = %s" % (inflow, DC,inflow/DC))
plt.plot(time,S_store)
plt.xlabel('Time (t)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/perturbation-big-flow.png")
plt.close()

Bottom line …

Dynamic equilibria that have small flows compared to stock sizes (for example because of a small decay constant) have large average residence times, and large response times.

Fluctuating systems

import numpy as np
import matplotlib.pyplot as plt
import math

DC = 0.5

# Configure time
t_end=120
dt=0.1
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy lists for numerical series
S_store=[] 
inflow_store=[]
# Initialise stock size
S = 100
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)

    inflow = 0.5 * math.sin(2 * math.pi * t / 30) + 50
    inflow_store.append(inflow)
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)


fig, ax1 = plt.subplots()

color = 'tab:blue'
ax1.set_xlabel('Time (t)')
ax1.set_ylabel('Stock Size', color=color)
ax1.plot(time, S_store, color=color)
ax1.tick_params(axis='y', labelcolor=color)
ax1.set_ylim([min(S_store), max(S_store)])

ax2 = ax1.twinx()
color = 'tab:red'
ax2.set_ylabel('Inflow', color=color)
ax2.plot(time, inflow_store, color=color)
ax2.tick_params(axis='y', labelcolor=color)
ax2.set_ylim([min(inflow_store), max(inflow_store)])

fig.tight_layout()
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/equilibria-fluctuation.png")
plt.close()

Fluctuations with slower response time

import numpy as np
import matplotlib.pyplot as plt
import math

DC = 0.05

# Configure time
t_end=120
dt=0.1
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy lists for numerical series
S_store=[] 
inflow_store=[]
# Initialise stock size
S = 99.77
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)

    inflow = 0.05 * math.sin(2 * math.pi * t / 30) + 5
    inflow_store.append(inflow)
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)


fig, ax1 = plt.subplots()

color = 'tab:blue'
ax1.set_xlabel('Time (t)')
ax1.set_ylabel('Stock Size', color=color)
ax1.plot(time, S_store, color=color)
ax1.tick_params(axis='y', labelcolor=color)
ax1.set_ylim([min(S_store), max(S_store)])

ax2 = ax1.twinx()
color = 'tab:red'
ax2.set_ylabel('Inflow', color=color)
ax2.plot(time, inflow_store, color=color)
ax2.tick_params(axis='y', labelcolor=color)
ax2.set_ylim([min(inflow_store), max(inflow_store)])

fig.tight_layout()
plt.grid(True)
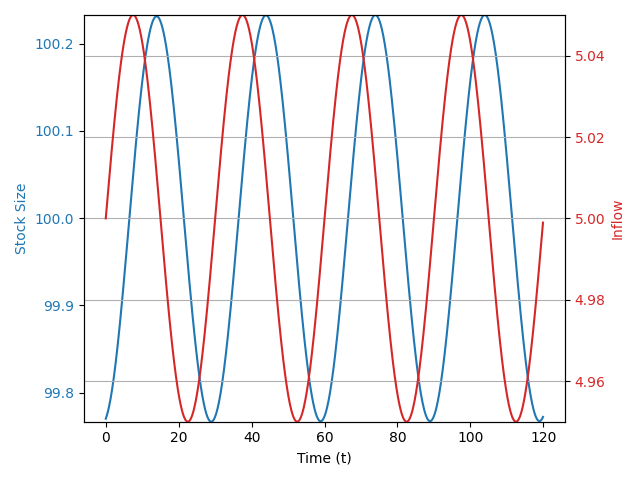
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/equilibria-fluctuation-slower.png")
plt.close()

Adding features

Connected systems

Feedback factors

Simple dynamic equilibrium with forcing

import matplotlib.pyplot as plt

inflow = 2
DC = 0.5

# Configure time
t_end=30
dt=0.1
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 3
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    if t == 10:
        inflow = inflow * 2

# PLOTTING
plt.title("Simple scenario")
plt.plot(time,S_store)
plt.xlabel('Time (t)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/feedback_simple.png")
plt.close()

Adding feedback

import matplotlib.pyplot as plt

inflow = 2

# Configure time
t_end=30
dt=0.1
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 3
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)
    # Calculate DC
    DC = 0.54-0.01*S
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    if t == 10:
        inflow = inflow * 2

# PLOTTING
plt.title("Adding feedback")
plt.plot(time,S_store)
plt.xlabel('Time (t)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/graph_with_feedback.png")
plt.close()

Feedback factor

Feedback factor lower than 1

In this case, the decay rate does not decrease with the stock size, but increase.

import matplotlib.pyplot as plt

inflow = 2

# Configure time
t_end=30
dt=0.1
time=np.arange(0,t_end,dt)

## NUMERICAL SOLUTION
# Create empy list for numerical series
S_store=[] 
# Initialise stock size
S = 3
# For every item in the List time
for t in time:
    # Append the new stock size
    S_store.append(S)
    # Calculate DC
    DC = 0.46+0.01*S
    # Calculate dS/dt
    dS=inflow-DC*S 
    # Multiply dS/dt with dt and add to stock size
    S=S+(dS*dt)
    if t == 10:
        inflow = inflow * 2

# PLOTTING
plt.title("Adding feedback")
plt.plot(time,S_store)
plt.xlabel('Time (t)')
plt.grid(True)
plt.savefig("/home/misha/Nextcloud/mnotes/mnotes_folders/presentations/images/graph_with_feedback2.png")
plt.close()

System Earth 1b

A planet in and out of equilibrium

Misha Velthuis

m.velthuis@uva.nl

Fri 6 Sept 2024

Recap

Content

Systems thinking

Tendency to focus on how things connect

Tendency to zoom out

Stocks and flows

Basics

Dynamic equilibria

Average residence time

Average residence time

We are all dynamic equilibria

Stocks influencing flows

Feedback loops

Positive feedback loop:

Negative feedback loop

Breaking down in couplings

Combining couplings

Spiral of love

Spiral of toxic comparison

Stability of a weird friendship

Stability of a reservoir

Stability of a reservoir

Recap of (part of) calculus

What is Euler's e?

The e of Earth: growth #1

The e of Earth: growth #2

The e of Earth: decay #1

The e of Earth: decay #2

Reservoir: constant inflow, variable outflow

Numerical solutions: the easy way out

Code in Python

Code in Python with graph

Compare numerical and analytic

Compare numerical and analytic

Perturbations and forcings

Response time

Let's see …

Bottom line …

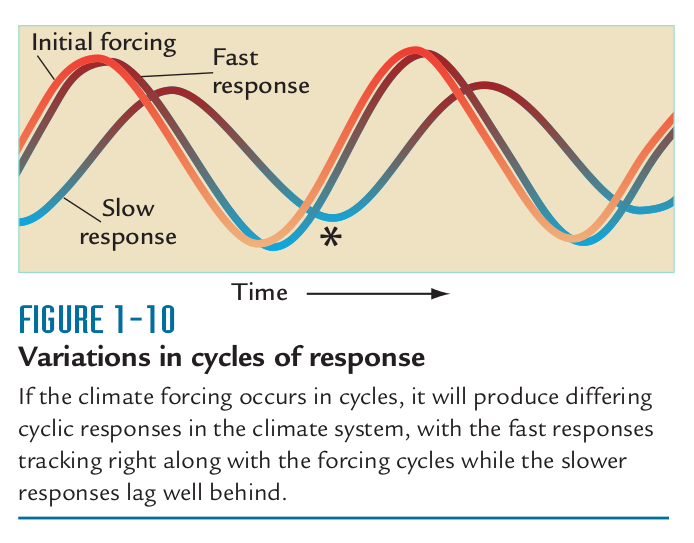
Fluctuating systems

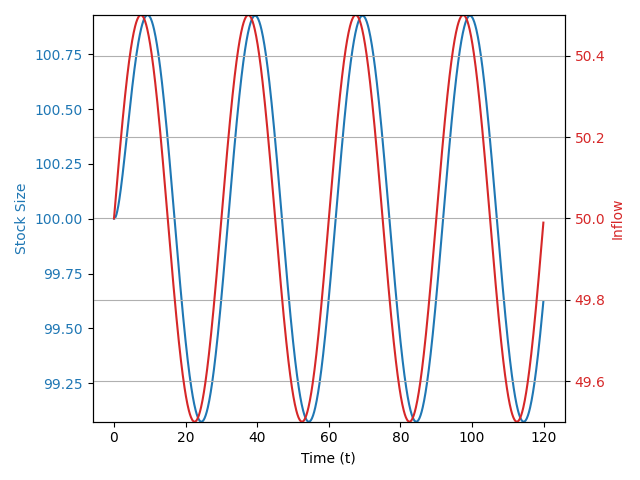
Fluctuations with slower response time

Adding features

Connected systems

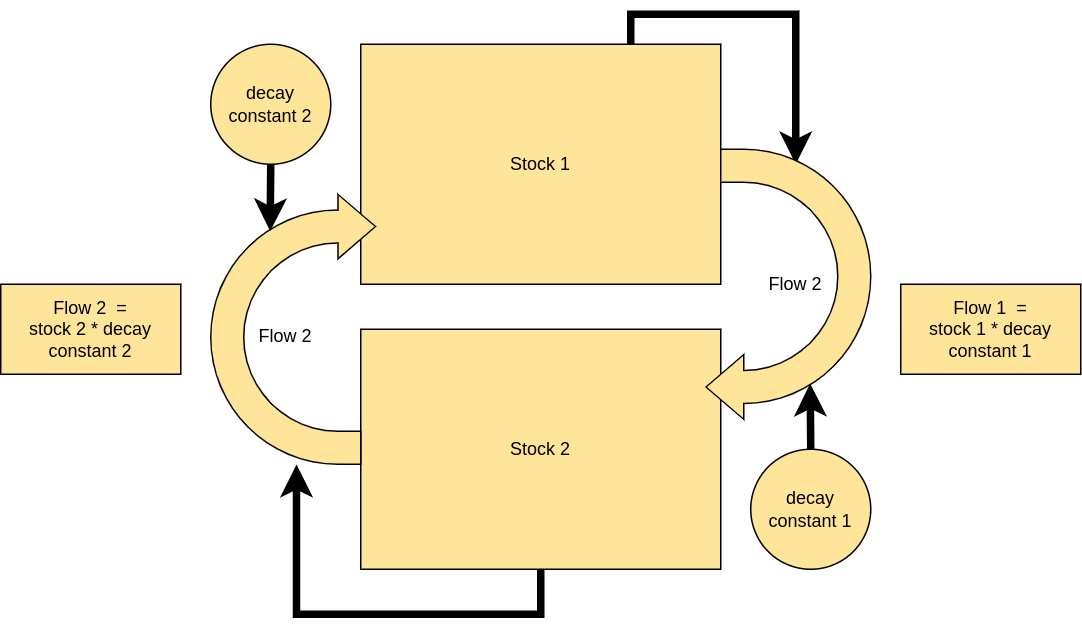
Feedback factors

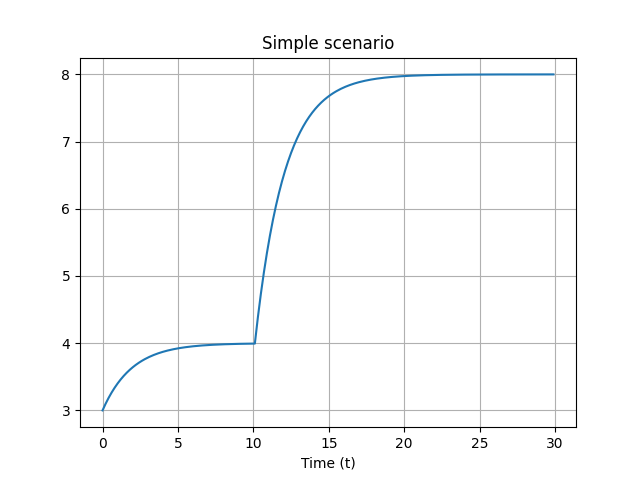
Simple dynamic equilibrium with forcing

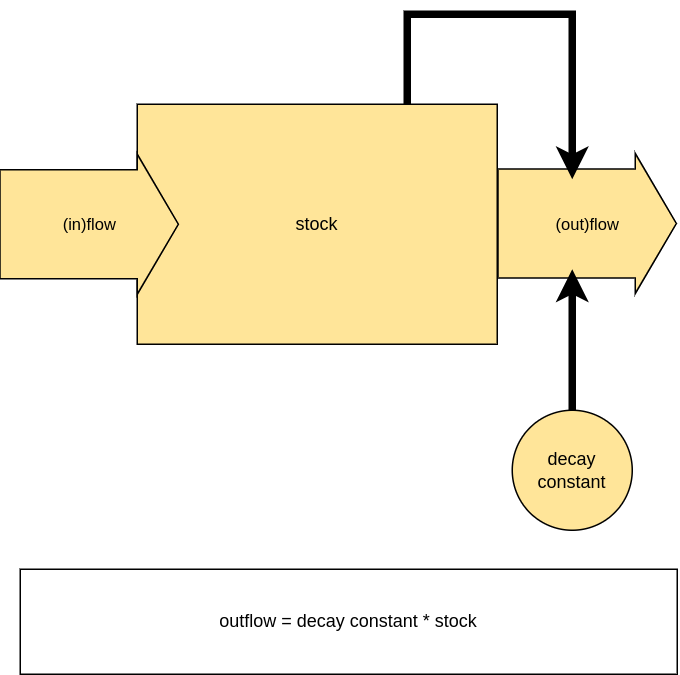
Simple dynamic equilibrium with forcing

Simple dynamic equilibrium with forcing

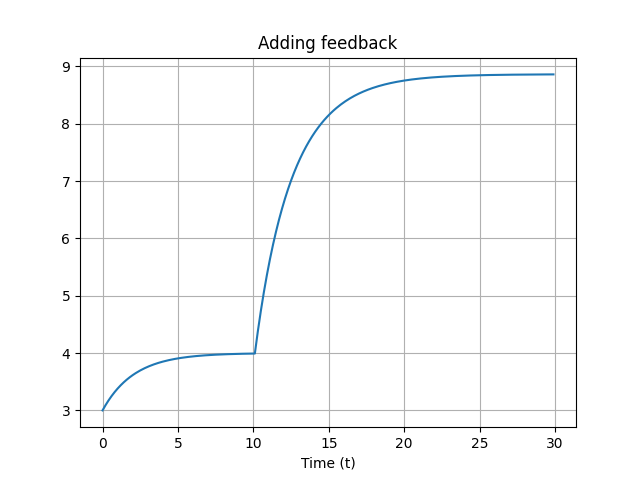
Adding feedback

Adding feedback

Feedback factor

Feedback factor lower than 1

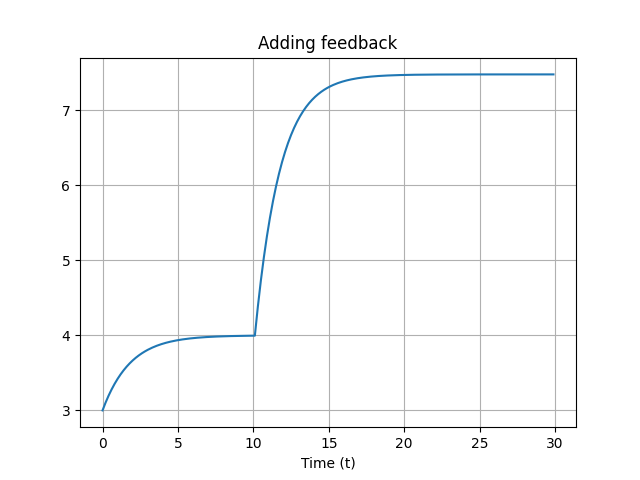
Gaia hypothesis