The basic set-up of the model¶
This is a simple model of how the Earth's surface absorbs shortwave radiation, and how this energy is sent back up in the form of longwave radiation.
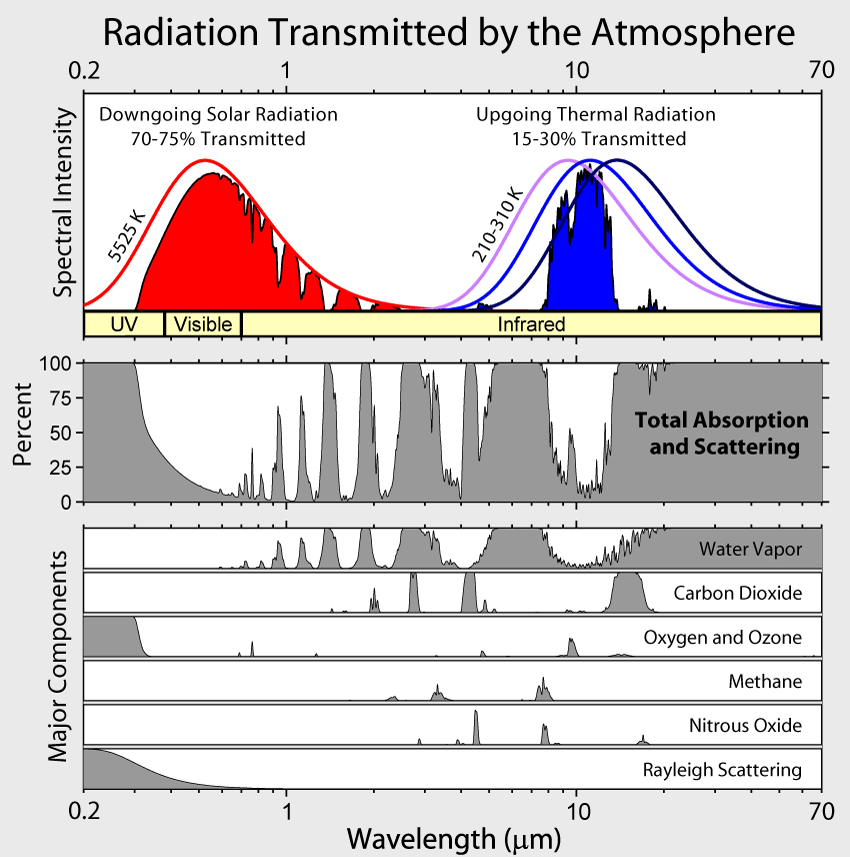
In this model I distinguish AW radiation (atmospheric window radiation) and NAW radiation (not atmospheric window radiation). See the image below for a visualization of the atmospheric window.
Every radiating element of the model (surface and atmosphere/ atmospheric layer) emits both AW radiation (25%) and NAW radiation (75%).
AW radiation is not absorbed by the atmosphere: downward AW radiation reaches (and is absorbed by) the surface without intervention of intermediary atmospheric layers, and upward AW radiation escapes to space.
NAW radiation is absorbed by surrounding atmospheric layers, following a certain absorbtion rate, and it is absorbed by the surface with a absorbation rate of 100%.
Following these rules, the radiation bounces back up and down.
As the original flux from sun bounces back and forth 1. between the the surface and the layers, and 2.between the layers among themselves, the fluxes become smaller, meaning that the sum of fluxes over time approximates an equilibrium.
Limitations¶
This is a very simplified model, to just explore this basic dynamic. There are unlimited limitations, some of which include:
- The model only simulates electromagnetic radiation. There are other ways in which the earth redistributes energy/heat vertically (e.g. convection, conduction).
- In this model, the atmosphere does not absorb any of the incoming shortwave radiation.
The code¶
Importing libraries¶
import matplotlib.pyplot as plt
import numpy as np
import math
Creating a layer class¶
Here I am defining a class called "Layer", with a method called "update_layer". Below, I create instances (objects) of this class, and add them to a list. Then I call the method "update_layer" on each of the objects.
class Layer:
# AW = atmopsheric window: the radiation of
# wavelengths that the atmosphere is transparant to
# NAW = the remaining part of the radiation that the
# atmosphere is not transparent to.
def __init__(self, pos):
# pos is the position of this Layer object in a list of Layer objects
self.pos = pos
self.outgoing_up = 0
self.outgoing_up_AW = 0
self.outgoing_up_NAW = 0
self.outgoing_down_AW = 0
self.outgoing_down_NAW = 0
self.outgoing_down = 0
self.incoming_store = []
self.temp_store = []
def update_layer(self):
# absorbtion is global so it can be defined
# outside of this function/class definition
global absorbtion
global atm_window
if atm_window == True:
AW_perc = 0.25
#print("true")
else:
AW_perc = 0
#print("false")
# The first few examples will have a constant absorbtion rate
# across the vertical profile
if constant_absorbtion == True:
absorbtion = [absorbtion_base for x in range(number_layers)]
else:
# In this formula, the absorbtion per layer starts at absorbtion_base in
# the bottom layer, and declines to half of the absorbtion_base in
# the top layer
absorbtion = [(1-(0.85/number_layers)*x)*absorbtion_base for x in range(number_layers)]
# Each round of updates, the incoming energy is set to 0, after which it will
# be built up from the outgoing energy from layers above and below
self.incoming = 0
self.incoming_from_below = 0
self.incoming_from_below_AW = 0
self.incoming_from_above = 0
# The surface absorbs a flux of 239 J.s^-1.m^-2
# (The self.pos goes upfrom 0 (surface)).
if self.pos == 0:
self.incoming_from_above = 239
# RADIATION FROM LAYERS BELOW
# Select layers 0 up to but not including itself.
for ind, layer in enumerate(layers[0:self.pos]):
# N.B.: I do not multiply with absorbtion yet here, so that I can use the unmodified
# "incoming_from_below" in the calculation of the temperature.
# This calculates what fraction of the NAW radiation emitted by the layer below reaches the
# layer under consideration.
pass_through = math.prod([(1-x) for x in absorbtion[layer.pos+1:self.pos]])
# This calculates how much of the outgoing_up_NAW reaches the layer. I do not
# multiply this with the absorbtion yet, so that I can use the unmodified
# "incoming_from_below" in the calculation of the temperature (where I need
# the part that passes through, rather than the part that is absorbed).
self.incoming_from_below = self.incoming_from_below + (layer.outgoing_up_NAW*pass_through)
# This calculates how much AW radiation reaches the layer. The atmosphere does
# not absorb AW radiation, it just reaches it. This is used in calculating the temperature
# that belongs to the total upward flux of each layer.
self.incoming_from_below_AW = self.incoming_from_below_AW + layer.outgoing_up_AW
# RADIATION FROM LAYERS ABOVE
# This part does not apply to the top layer, because it does not receive anything from above.
if self.pos < (number_layers-1):
# Select layers self.pos+1 up to the end, and enumerate it, so that the layer directly above gets the ind 0
for ind, layer in enumerate(layers[self.pos+1:]):
# This calculates what fraction of the radiation emitted by a layer above reaches the
# layer under consideration.
pass_through = math.prod([(1-x) for x in absorbtion[self.pos+1:layer.pos]])
# The surface receives all outgoing_down_AW from all overlying layers.
# The surface also receives outgoing_down_NAW from overlying layers, but only the
# part that is not absorbed by the layers in between.
# Reminder #: the surface absorbs 100 %...
if self.pos == 0:
self.incoming_from_above = self.incoming_from_above + (layer.outgoing_down_NAW*pass_through) + layer.outgoing_down_AW
else:
# A layer does not receive any outgoing_down_AW because the atmosphere is transparent for this radiation.
# A layer does receive outgoing down_NAW but only the part that it absorbs.
self.incoming_from_above = self.incoming_from_above + \
absorbtion[self.pos]*layer.outgoing_down_NAW*pass_through
self.incoming = (absorbtion[self.pos]*self.incoming_from_below) + self.incoming_from_above
# If the layer is the surface, all incoming radiation becomes outgoing_up
if self.pos == 0:
self.outgoing_up = self.incoming
self.outgoing_up_AW = self.incoming*AW_perc
self.outgoing_up_NAW = self.incoming*(1-AW_perc)
# For all other layers, energy radiates upwards and downwards
else:
self.outgoing_up = self.incoming/2
self.outgoing_up_AW = self.outgoing_up*AW_perc
self.outgoing_up_NAW = self.outgoing_up*(1-AW_perc)
self.outgoing_down = self.incoming/2
self.outgoing_down_AW = self.outgoing_down*AW_perc
self.outgoing_down_NAW = self.outgoing_down*(1-AW_perc)
# Each layer radiates energy to space (just for the sake of keeping track)
# This is calculated with the NAW-radiation emitted upwards, reduced by the amount of absorbtion
# by the layers in between plus the AW-radiation (that is not absorbed by the layers in between).
self.to_space = self.outgoing_up_NAW*(math.prod([(1-x) for x in absorbtion[self.pos+1:]]))+self.outgoing_up_AW
# Calculate temperature per layer. I am calculating the temperature as felt "from above".
# So that means the radiation that is absorbed (from above and below) and re-emitted upwards
# by the layer *plus* the radiation (Both NAW and AW) that passes from blow, upwards through the the layer.
self.temp = ((self.outgoing_up+(self.incoming_from_below*(1-absorbtion[self.pos]))+self.incoming_from_below_AW)/SBC)**(1/4)
# Store incoming energy and temperature
self.incoming_store.append(self.incoming)
self.temp_store.append(self.temp)
Adding some constants¶
# Stefan Boltzmann constant
SBC = 5.670374419*(10**-8)
time = range(50)
Run and plot function¶
def run_and_plot():
# This makes it possible to use the variable "layers"
# in the other function.
global layers
# Create the layers
layers = []
for x in range(number_layers):
layers.append(Layer(x))
# Running model
for t in time:
space_layers = []
for ind, layer in enumerate(layers):
layer.update_layer()
# list of energy lost to space per layer
space_layers.append(layer.to_space)
# taking space_layers of last model run, and sum up energy lost of those layers
sum_space_tot = sum(space_layers)
# create a list that shows what fraction of total energy lost is lost per layer
sum_space_part = [x / sum_space_tot for x in space_layers]
print(f'Total energy sent back to space (sum_space_tot) {round(sum_space_tot,2)} W.m-2.s-2')
#-----------------------------
# Plotting
#-----------------------------
plot_layers_temp = [x.temp_store for x in layers]
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
# First subplot for the line plots
for ind, temp_in_kelvin in enumerate(plot_layers_temp):
if ind == 0:
axs[0].plot(time, temp_in_kelvin, label="Surface")
else:
axs[0].plot(time, temp_in_kelvin, label=f"Layer {ind}")
y1, y2 = axs[0].get_ylim()
x1, x2 = axs[0].get_xlim()
ax2 = axs[0].twinx()
ax2.set_ylim(y1 - 273.15, y2 - 273.15)
ax2.set_yticks(range(int(y1 - 273.15), int(y2 - 273.15), 10))
ax2.set_ylabel('Temp in °C')
ax2.set_xlim(x1, x2)
axs[0].set_ylabel('Temp in °K')
axs[0].set_xlabel('Time')
axs[0].legend()
# Annotate the final value on the graph
final_values = [temps[-1] for temps in plot_layers_temp]
for ind, final_value in enumerate(final_values):
label = f'{round(final_value, 2)} K' if ind == 0 else f'{round(final_value, 2)} K'
axs[0].annotate(label, (time[-1], final_value), textcoords="offset points", xytext=(-10, 5), ha='center', fontsize=6)
# Second subplot for bar plot
xticklabels = ['surface'] + [str(i) for i in np.arange(1, len(sum_space_part))]
axs[1].bar(xticklabels, sum_space_part)
axs[1].set_xlabel('Origin of energy loss')
axs[1].set_ylabel('Value')
axs[0].set_title("Temp different layers")
axs[1].set_title("Fraction of total energy loss to space by surface/layers")
plt.tight_layout()
plt.show()
Playing¶
Testing the one-layer atmosphere model¶
Without atmospheric window¶
Without implementing the transparency of the atmospheric window (i.e. the atmosphere absorbs 100% of all radiation) and with a one-layered atmosphere, the model reproduces the numbers mentioned by Kump et al:
255°K at the top of the atmosphere, and 303°K at the surface.
number_layers = 2 # # this means the model is divided in one surface layer and 1 atmospheric layer
absorbtion_base = 1 # this means that every layer absorbs 100% of the NAW radiation it receives
constant_absorbtion = True # this means that the absorbtion is constant across the vertical profile
atm_window = False # this means that we are not implementing the atmospheric window.
run_and_plot()
Total energy sent back to space (sum_space_tot) 239.0 W.m-2.s-2
With atmospheric window¶
If we then add the transparency of the atmospheric window, the surface temperature does indeed go down as Kump et al. predicted. To to 13.4° (286.6°K).
number_layers = 2 # # this means the model is divided in one surface layer and 1 atmospheric layer
absorbtion_base = 1 # this means that every layer absorbs 100% of the NAW radiation it receives
constant_absorbtion = True # this means that the absorbtion is constant across the vertical profile
atm_window = True # this means that we are implementing the atmospheric window.
run_and_plot()
Total energy sent back to space (sum_space_tot) 239.0 W.m-2.s-2
Adding layers¶
Let us now add more layers.
If we just add more atmospheric layers, without adjusting the percentage of the NAW radiation that is absorbed per layer (still 100%), the surface temperature goes up. I think this is what Kump et al. meant when they said that cutting the atmosphere up in more layers increases the greenhouse effect.
number_layers = 3 # this means the model is divided in one surface layer and 2 atmospheric layers
absorbtion_base = 1 # this means that every layer absorbs 70% of the NAW radiation it receives
constant_absorbtion = True # this means that the absorbtion is constant across the vertical profile
atm_window = True # this means that we are implementing the atmospheric window.
run_and_plot()
Total energy sent back to space (sum_space_tot) 239.0 W.m-2.s-2
Adding layers, adding transparency¶
In principle, cutting the atmosphere up in more layers should not increase the surface temperature: we are simply modelling the atmosphere at a higher resolution.
We can adjust the absorbtion rate per layer to prevent the increasing number of layers from causing the surface temperature to go up:
number_layers = 6 # this means the model is divided in one surface layer and 9 atmospheric layers
absorbtion_base = 0.39 # this is the percentage of NAW radiation that every layer absorbs
print((1-absorbtion_base)**(number_layers-1)) # This is the transparency for NAW radiation of the atmosphere as a whole
constant_absorbtion = True # this means that the absorbtion is constant across the vertical profile
atm_window = True # this means that we are implementing the atmospheric window.
run_and_plot()
0.08445963009999999 Total energy sent back to space (sum_space_tot) 239.0 W.m-2.s-2
With 6 layers (surface + 5 atmospheric layers) we need to lower the absorbtion rate per layer to 39% in order to still get a surface temperature of 288°K.
For the atmosphere as a whole this would mean that (1-0.39)^5=0.084 = 8.4% of the NAW radiation that leaves the surface can directly escape to space.
- For 10 layers, the absorbtion rate would have to be 24% to get to a surface temperature of 288°K, which would mean that 8.5% of the NAW radiation that leaves the surface can directly escape to space.
- For 20 layers, the absorbtion rate would have to be 12% to get to a surface temperature of 288°K, which would mean that 8.8% of the NAW radiation that leaves the surface can directly escape to space.
These percentages (around 8%) are a bit high... The atmosphere should be practically intransparent to NAW radiation from the surface.
Adding layers, varying transparency¶
Adding a little bit of extra complexity might help us out here.
Instead of using a constant absorbtion rate, we use an absorbtion rate that goes down as we go up towards the top layer.
This declining absorbtion rate could be understood as the declining amount of CO2 higher up in the atmosphere (due to lower air pressue).
If we for example start at an absorbtion rate of 0.65 at the bottom layer, and go down to 0.2 at the top layer, we also get a surface temperature of 288°K.
In this scenario, the atmosphere has an overall transparency for NAW radiation emanating from the surface of 0.34% (so 99.66 % is absorbed by the atmosphere).
That is more like it.
number_layers = 6 # this means the model is divided in one surface layer and 5 atmospheric layers
absorbtion_base = 0.65 # this is the percentage of NAW radiation that every layer absorbs
constant_absorbtion = False # this means that the absorbtion is not constant across the vertical profile
atm_window = True # this means that we are implementing the atmospheric window.
run_and_plot()
print("-----------\nOverall fraction of radiation from surface escaping to space: %s." % (round(math.prod(absorbtion),4)))
print("-----------\nOverall percentage of radiation from surface escaping to space: %s percent.\n-----------" % (round(100*math.prod(absorbtion),2)))
fig, ax = plt.subplots()
plt.title("Aborbtion vs layer index")
ax.plot(absorbtion, range(number_layers))
# Add axis labels and title
ax.set_xlabel('Absorbtion percentage of individual layers')
ax.set_ylabel('Layer index')
ax.set_title('Absorbtion vs layer index')
Total energy sent back to space (sum_space_tot) 239.0 W.m-2.s-2
----------- Overall fraction of radiation from surface escaping to space: 0.0034. ----------- Overall percentage of radiation from surface escaping to space: 0.34 percent. -----------
Text(0.5, 1.0, 'Absorbtion vs layer index')
Enhanced greenhouse effect¶
To simulate the enhanced greenhouse effect, we can "simply" increase the absorbtion rate of each layer a bit.
The atmosphere as a whole is still practically impermeable for the NAW radiation emanating from the surface, but higher up, where NAW radiation normally escapes more easily to space, it now becomes harder for NAW radiation to escape to space.
As a result the surface temperature goes up.
number_layers = 6 # this means the model is divided in one surface layer and 5 atmospheric layers
absorbtion_base = 0.65*1.2 # this is the percentage of NAW radiation that every layer absorbs + enhanced greenhouse effect
constant_absorbtion = False # this means that the absorbtion is constant across the vertical profile
atm_window = True # this means that we are implementing the atmospheric window.
run_and_plot()
fig, ax = plt.subplots()
ax.plot(absorbtion, range(number_layers))
# Add axis labels and title
ax.set_xlabel('Absorbtion percentage of individual layers')
ax.set_ylabel('Layer index')
ax.set_title('Absorbtion vs layer index')
Total energy sent back to space (sum_space_tot) 239.0 W.m-2.s-2
Text(0.5, 1.0, 'Absorbtion vs layer index')